Usage

continuum_mechanics relies on SymPy for symbolic calculations. To use Continuum Mechanics in a project you can import it as:

import continuum_mechanics

Vector operators in Cartesian coordinates

https://mybinder.org/badge_logo.svg

continuum_mechanics support major vector operators such as:

  • gradient of a scalar function;
  • divergence of a vector function;
  • curl of a vector function;
  • gradient of a vector function;
  • divergence of a tensor;
  • Laplace operator of a scalar function;
  • Laplace operator of a vector function; and
  • Biharmonic operator of a scalar function.

All these operators are in the module vector.

from sympy import *
from continuum_mechanics import vector

By default, Cartesian coordinates are given by \(x\), \(y\) and \(z\). If these coordinates are used there is not necessary to specify them when calling the vector operators

init_printing()
x, y, z = symbols("x y z")

Following, we have some examples of vector operators in Cartesian coordinates.

Gradient of a scalar function

The gradient takes as input a scalar and returns a vector, represented by a 3 by 1 matrix.

f = 2*x + 3*y**2 - sin(z)
f
\[2 x + 3 y^{2} - \sin{\left (z \right )}\]
vector.grad(f)
\[\begin{split}\left[\begin{matrix}2\\6 y\\- \cos{\left (z \right )}\end{matrix}\right]\end{split}\]

Divergence of a vector function

The divergence takes as input a vector (represented by a 3 by 1 matrix) and returns a scalar.

vector.div(Matrix([x, y, z]))
\[3\]
vector.div(Matrix([
    x**2 + y*z,
    y**2 + x*z,
    z**2 + x*y]))
\[2 x + 2 y + 2 z\]

Divergence of a tensor function

The divergence of a tensor (represented by a 3 by 3 matrix) returns a vector.

Axx, Axy, Axz = symbols("A_xx A_xy A_xz", cls=Function)
Ayx, Ayy, Ayz = symbols("A_yx A_yy A_yz", cls=Function)
Azx, Azy, Azz = symbols("A_zx A_zy A_zz", cls=Function)

tensor = Matrix([
    [Axx(x, y, z), Axy(x, y, z), Axz(x, y, z)],
    [Ayx(x, y, z), Ayy(x, y, z), Ayz(x, y, z)],
    [Azx(x, y, z), Azy(x, y, z), Azz(x, y, z)]])
tensor
\[\begin{split}\begin{bmatrix} A_{xx}(x,y,z) & A_{xy}(x,y,z) & A_{xz}(x,y,z)\\ A_{yx}(x,y,z) & A_{yy}(x,y,z) & A_{yz}(x,y,z)\\ A_{zx}(x,y,z) & A_{zy}(x,y,z) & A_{zz}(x,y,z) \end{bmatrix}\end{split}\]
vector.div_tensor(tensor)
\[\begin{split}\left[\begin{matrix} \frac{\partial}{\partial x} A_{xx}(x, y, z) + \frac{\partial}{\partial y} A_{xy}(x, y, z) + \frac{\partial}{\partial z} A_{xz}(x, y, z)\\ \frac{\partial}{\partial x} A_{yx}(x, y, z) + \frac{\partial}{\partial y} A_{yy}(x, y, z) + \frac{\partial}{\partial z} A_{yz}(x, y, z)\\ \frac{\partial}{\partial x} A_{zx}(x, y, z) + \frac{\partial}{\partial y} A_{zy}(x, y, z) + \frac{\partial}{\partial z} A_{zz}(x, y, z) \end{matrix}\right]\end{split}\]

Curl of a vector function

Let us check the identity

\[\nabla \times \nabla f(x, y, z) = 0\, .\]
fun = symbols("fun", cls=Function)
vector.curl(vector.grad(fun(x, y, z)))
\[\begin{split}\left[\begin{matrix}0\\0\\0\end{matrix}\right]\end{split}\]

Visualization of tensors

from sympy import Matrix
from continuum_mechanics.visualization import mohr2d, mohr3d, traction_circle

Visualization in 2D

First, let us visualize the tensor

\[\begin{split}\begin{bmatrix} 1 &0\\ 0 &-1 \end{bmatrix}\, .\end{split}\]
mohr2d(Matrix([
  [1,0],
  [0,-1]]))
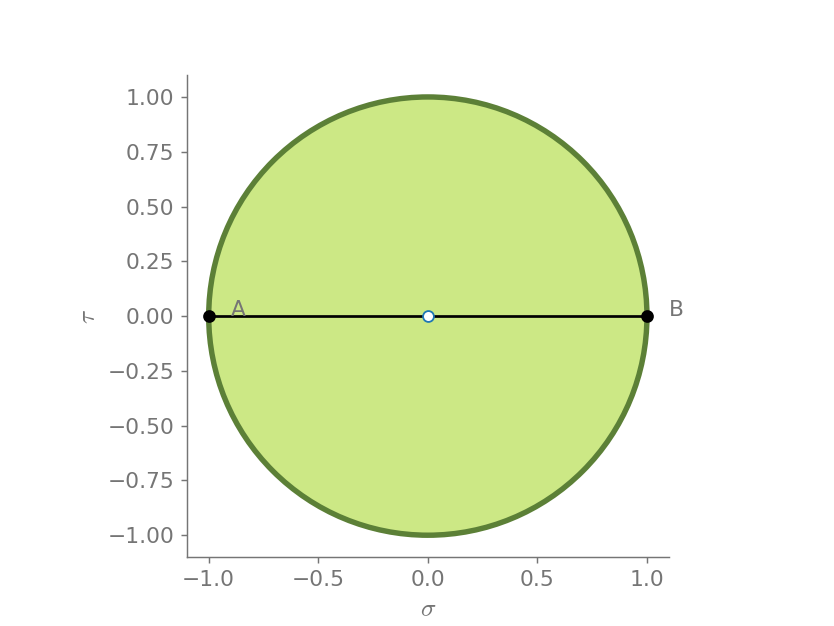
_images/mohr2d_1.png

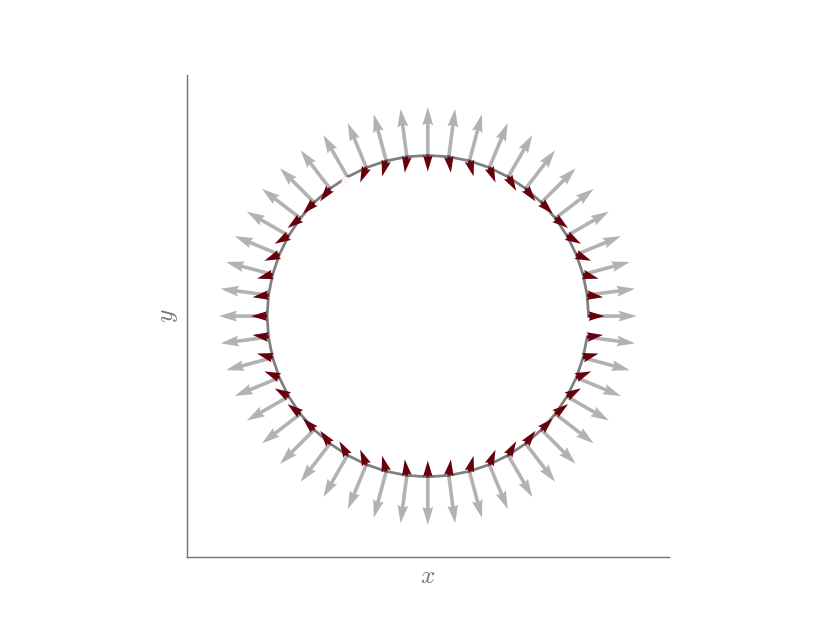
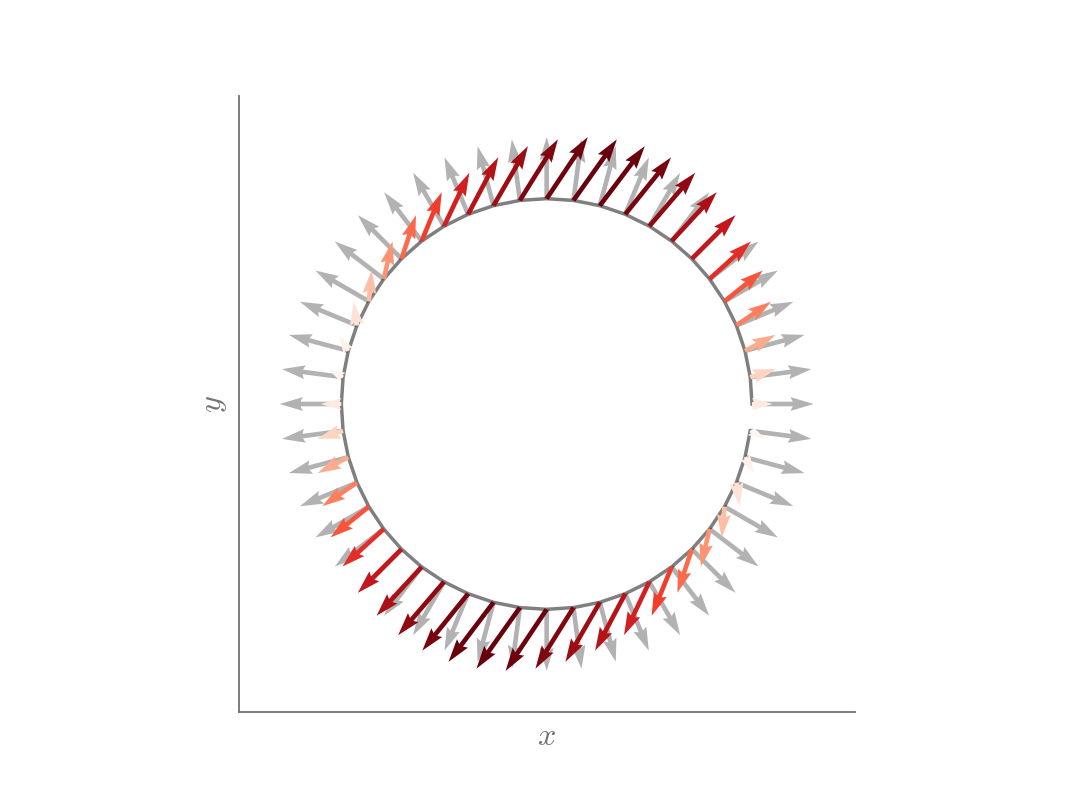
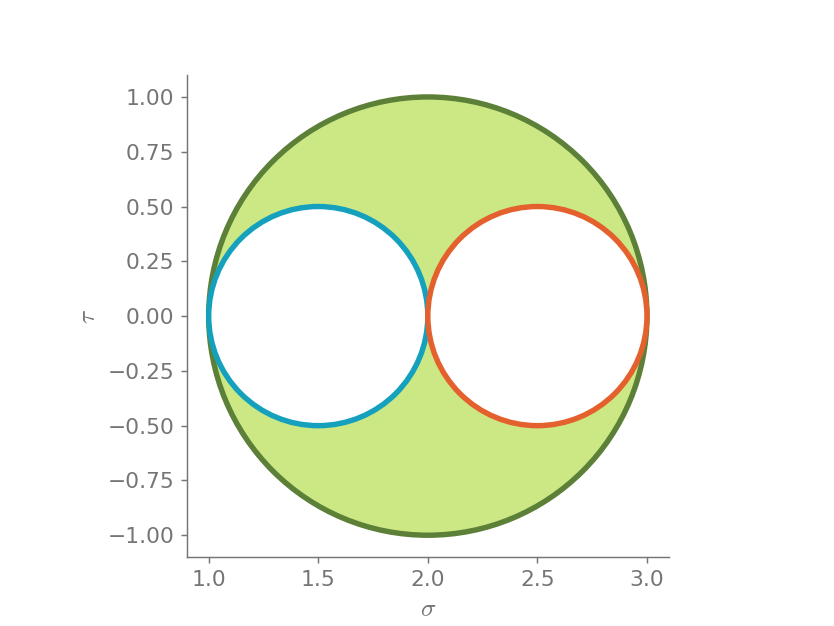
From the Mohr circle, we can see that the principal directions are given at \(0\) and \(\pi/2\) radians. This can be more easily visualized using the traction circle, where normal vectors are presented in light gray and the traction vectors are presented in colors.

traction_circle(Matrix([
  [1,0],
  [0,-1]]))
_images/trac2d_1.png

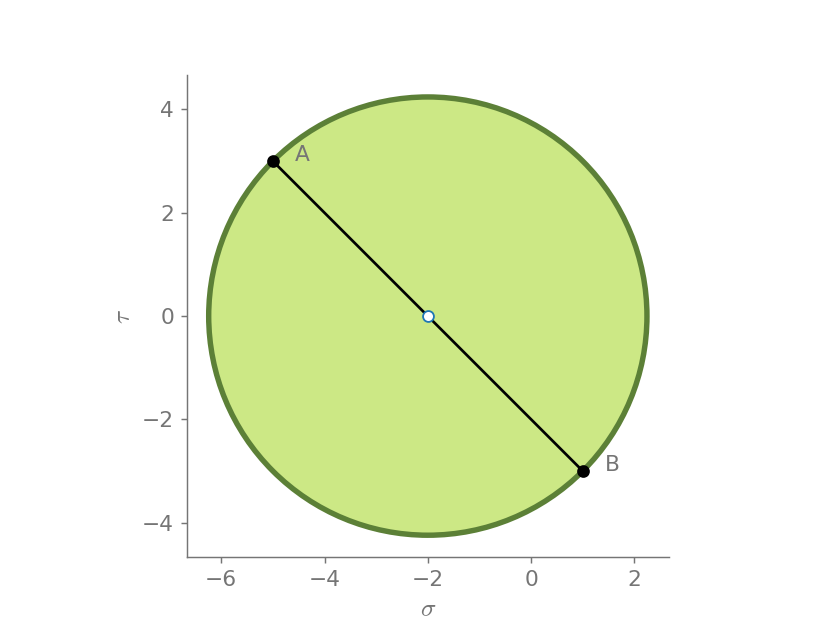
Now, let us visualize

\[\begin{split}\begin{bmatrix} 1 &3\\ 3 &-5 \end{bmatrix}\, .\end{split}\]
mohr2d(Matrix([
  [1, 3],
  [3, -5]]))
_images/mohr2d_2.png 
traction_circle(Matrix([
  [1, 3],
  [3, -5]]))
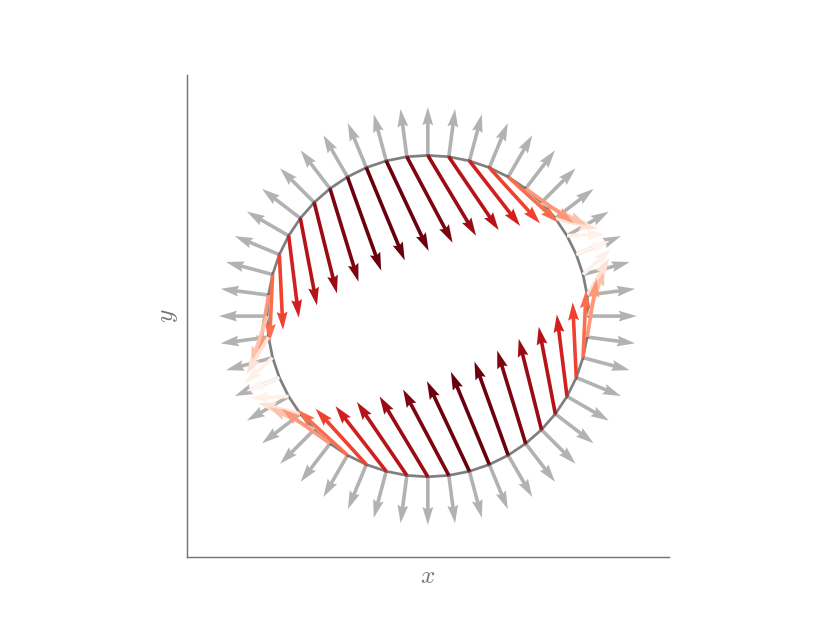
_images/trac2d_2.png

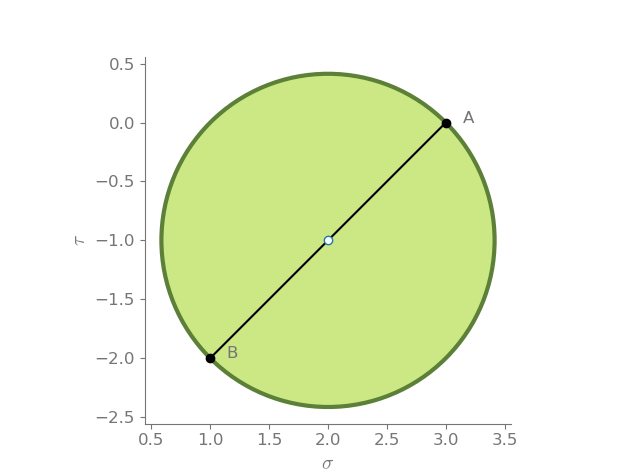
Now, let us try it with an asymmetric tensor

\[\begin{split}\begin{bmatrix} 1 &2\\ 0 &3 \end{bmatrix}\, .\end{split}\]
mohr2d(Matrix([
  [1, 2],
  [0, 3]]))
_images/mohr2d_3.png 
traction_circle(Matrix([
  [1, 2],
  [0, 3]]))
_images/trac2d_3.png

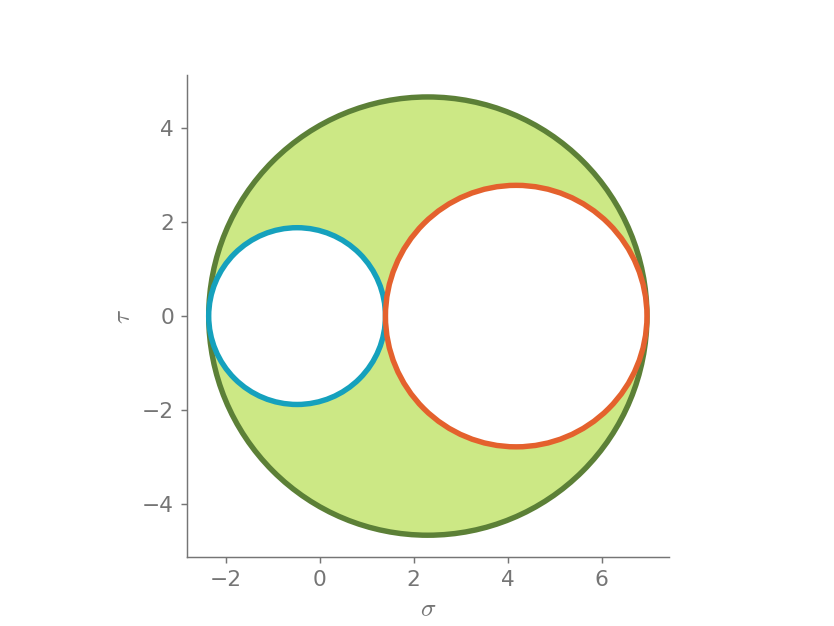
Mohr Circle in 3D

Let us visualize the tensor

\[\begin{split}\begin{bmatrix} 1 &2 &4\\ 2 &2 &1\\ 4 &1 &3 \end{bmatrix}\, .\end{split}\]
mohr3d(Matrix([
    [1, 2, 4],
    [2, 2, 1],
    [4, 1, 3]]))
_images/mohr3d_1.png

Now, let us visualize the tensor

\[\begin{split}\begin{bmatrix} 1 &0 &0\\ 0 &2 &0\\ 0 &0 &3 \end{bmatrix}\, .\end{split}\]
mohr3d(Matrix([
    [1, 0, 0],
    [0, 2, 0],
    [0, 0, 3]]))
_images/mohr3d_2.png

Elasticity tensor visualization

Let us consider β-brass that is a cubic material and has the following material properties in Voigt notation:

\[C_{11} = 52\text{ GPa},\quad C_{12} = 27.5\text{ GPa},\quad C_{44} = 173\text{ GPa}.\]
C11 = 52e9
C12 = 27.5e9
C44 = 173e9
rho = 7600
C = np.zeros((6, 6))
C[0:3, 0:3] = np.array([[C11, C12, C12],
                        [C12, C11, C12],
                        [C12, C12, C11]])
C[3:6, 3:6] = np.diag([C44, C44, C44])

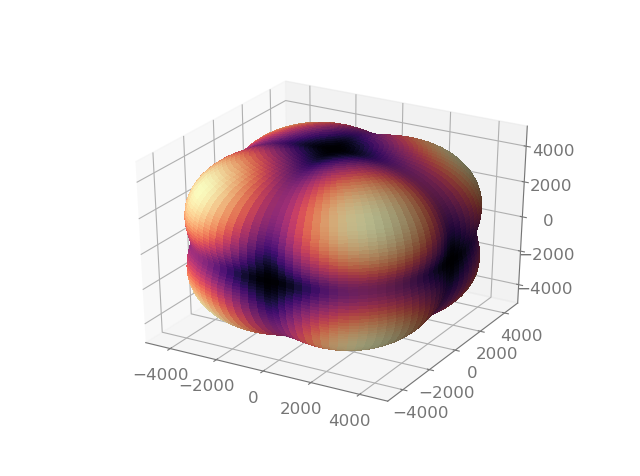
One way to visualize a stiffness tensor is to use the Christofel equation

\[\det(\Gamma_{ij} - v_p^2\delta_{ij}) = 0\, ,\]

where \(\Gamma_{ij}\) is the Christofel stiffness and depends on the material properties (\(c_{ijkl}\)) and unit vectors (:math`n_i`):

This provides the eigenvalues that represent the phase speed for three propagation modes in the material.

V1, V2, V3, phi_vec, theta_vec = christofel_eig(C, 100, 100)
V1 = np.sqrt(V1/rho)
V2 = np.sqrt(V2/rho)
V3 = np.sqrt(V3/rho)

Phase speed for the first quasi-transverse mode.

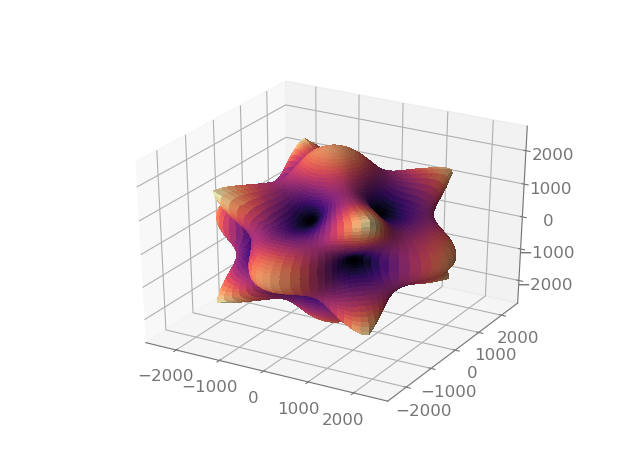
_images/qS1.png

Phase speed for the second quasi-transverse mode.

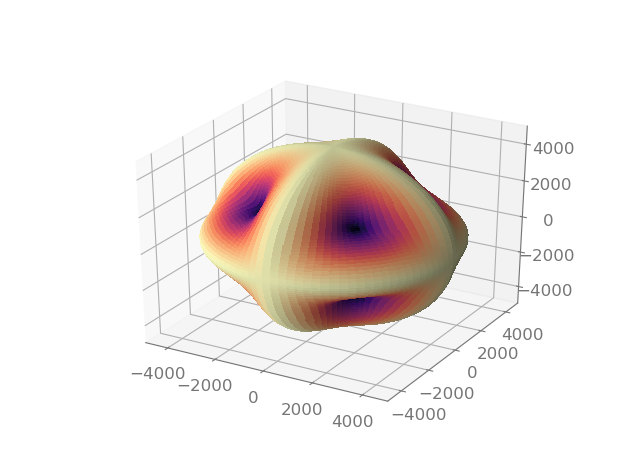
_images/qS2.png

Phase speed for the quasi-longitudinal mode.

_images/qP.png