Point source on top of a halfspace

import numpy as np
from sympy import init_printing, symbols, lambdify, S, simplify
from sympy import pi, Matrix, sqrt, oo
from continuum_mechanics.solids import sym_grad, strain_stress

import matplotlib.pyplot as plt
from matplotlib import colors

The following snippet allows to format the graphs.

repo = "https://raw.githubusercontent.com/nicoguaro/matplotlib_styles/master"
style = repo + "/styles/minimalist.mplstyle"
plt.style.use(style)

x, y, z, r, E, nu, Fx, Fy, Fz = symbols('x y z r E nu F_x F_y F_z')

The components of the displacement vector are given by [LANDAU]_
\[\begin{split}\begin{align} &u_x = \frac{(1 + \nu)}{2 \pi E} \left\{\left[\frac{xz}{r^3} - \frac{(1 - 2\nu)x}{r(r + z)}\right]F_z + \frac{2(1 - \nu)r +z}{r(r + z)}F_x +\frac{[2r(\nu r + z) + z^2]x}{r^3(r + z)^2}(xF_x + y F_y)\right\}\, ,\\ &u_y = \frac{(1 + \nu)}{2 \pi E} \left\{\left[\frac{yz}{r^3} - \frac{(1 - 2\nu)y}{r(r + z)}\right]F_z + \frac{2(1 - \nu)r +z}{r(r + z)}F_y +\frac{[2r(\nu r + z) + z^2]y}{r^3(r + z)^2}(xF_x + y F_y)\right\}\, ,\\ &u_z = \frac{(1 + \nu)}{2 \pi E} \left\{\left[\frac{2(1 - \nu)}{r} - \frac{z^2}{r^3}\right]F_z +\left[\frac{1 - 2\nu}{r(r + z)} + \frac{z}{r^3}\right](xF_x + y F_y)\right\}\, , \end{align}\end{split}\]

with \(r = \sqrt{x^2 + y^2 + z^2}\).

ux = (1+nu)/(2*pi*E)*((x*z/r**3 - (1-2*nu)*x/(r*(r + z)))*Fz +
                       (2*(1 - nu)*r + z)/(r*(r + z))*Fx +
                       ((2*r*(nu*r + z) + z**2)*x)/(r**3*(r + z)**2)*(x*Fx + y*Fy))
ux
\[\frac{1}{2 \pi E} \left(\nu + 1\right) \left(\frac{F_{x}}{r \left(r + z\right)} \left(r \left(- 2 \nu + 2\right) + z\right) + F_{z} \left(- \frac{x \left(- 2 \nu + 1\right)}{r \left(r + z\right)} + \frac{x z}{r^{3}}\right) + \frac{x}{r^{3} \left(r + z\right)^{2}} \left(F_{x} x + F_{y} y\right) \left(2 r \left(\nu r + z\right) + z^{2}\right)\right)\]
uy = (1+nu)/(2*pi*E)*((y*z/r**3 - (1-2*nu)*y/(r*(r + z)))*Fz +
                       (2*(1 - nu)*r + z)/(r*(r + z))*Fy +
                       ((2*r*(nu*r + z) + z**2)*y)/(r**3*(r + z)**2)*(x*Fx + y*Fy))
uy
\[\frac{1}{2 \pi E} \left(\nu + 1\right) \left(\frac{F_{y}}{r \left(r + z\right)} \left(r \left(- 2 \nu + 2\right) + z\right) + F_{z} \left(- \frac{y \left(- 2 \nu + 1\right)}{r \left(r + z\right)} + \frac{y z}{r^{3}}\right) + \frac{y}{r^{3} \left(r + z\right)^{2}} \left(F_{x} x + F_{y} y\right) \left(2 r \left(\nu r + z\right) + z^{2}\right)\right)\]
uz = (1+nu)/(2*pi*E)*((2*(1 - nu)/r + z**2/r**3)*Fz +
                       ((1 - 2*nu)/(r*(r + z)) + z/r**3)*(x*Fx + y*Fy))
uz
\[\frac{1}{2 \pi E} \left(\nu + 1\right) \left(F_{z} \left(\frac{1}{r} \left(- 2 \nu + 2\right) + \frac{z^{2}}{r^{3}}\right) + \left(F_{x} x + F_{y} y\right) \left(\frac{- 2 \nu + 1}{r \left(r + z\right)} + \frac{z}{r^{3}}\right)\right)\]

Withouth loss of generality we can assume that \(F_y=0\), this is equivalent a rotate the axes until the force is in the plane \(y=0\).

ux = ux.subs(Fy, 0)
ux
\[\frac{1}{2 \pi E} \left(\nu + 1\right) \left(\frac{Fx}{r \left(r + z\right)} \left(r \left(- 2 \nu + 2\right) + z\right) + \frac{Fx x^{2}}{r^{3} \left(r + z\right)^{2}} \left(2 r \left(\nu r + z\right) + z^{2}\right) + Fz \left(- \frac{x \left(- 2 \nu + 1\right)}{r \left(r + z\right)} + \frac{x z}{r^{3}}\right)\right)\]
uy = ux.subs(Fy, 0)
uy
\[\frac{1}{2 \pi E} \left(\nu + 1\right) \left(\frac{Fx}{r \left(r + z\right)} \left(r \left(- 2 \nu + 2\right) + z\right) + \frac{Fx x^{2}}{r^{3} \left(r + z\right)^{2}} \left(2 r \left(\nu r + z\right) + z^{2}\right) + Fz \left(- \frac{x \left(- 2 \nu + 1\right)}{r \left(r + z\right)} + \frac{x z}{r^{3}}\right)\right)\]
uz = uz.subs(Fy, 0)
uz
\[\frac{1}{2 \pi E} \left(\nu + 1\right) \left(Fx x \left(\frac{- 2 \nu + 1}{r \left(r + z\right)} + \frac{z}{r^{3}}\right) + Fz \left(\frac{1}{r} \left(- 2 \nu + 2\right) + \frac{z^{2}}{r^{3}}\right)\right)\]

The displacement vector is then

u = Matrix([ux, uy, uz]).subs(r, sqrt(x**2 + y**2 + z**2))

We can check that the displacement vanish when \(x,y,z \rightarrow \infty\)

u.limit(x, oo)
\[\begin{split}\left[\begin{matrix}0\\0\\0\end{matrix}\right]\end{split}\]
u.limit(y, oo)
\[\begin{split}\left[\begin{matrix}0\\0\\0\end{matrix}\right]\end{split}\]
u.limit(z, oo)
\[\begin{split}\left[\begin{matrix}0\\0\\0\end{matrix}\right]\end{split}\]

We can compute the strain and stress tensors using the symmetric gradient (vector.sym_grad()) and strain-to-stress (solids.strain_stress()) functions.

lamda = E*nu/((1 + nu)*(1 - 2*nu))
mu = E/(2*(1 - nu))
strain = sym_grad(u)
stress = strain_stress(strain, [lamda, mu])

The expressions for strains and stresses are lengthy and difficult to work with. Nevertheless, we can work with them. For example, we can evaluate the stress tensor at a point \(\mathbf{x} = (1, 0, 1)\) for a vertical load and a Poisson coefficient \(\nu = 1/4\).

simplify(stress.subs({x: 1, y: 0, z:1, nu: S(1)/4, Fx: 0}))
\[\begin{split}\left[\begin{matrix}- \frac{F_{z} \left(73 \sqrt{2} + 108\right)}{48 \pi \left(7 + 5 \sqrt{2}\right)} & - \frac{5 F_{z} \left(2 \sqrt{2} + 3\right)}{24 \pi \left(7 + 5 \sqrt{2}\right)} & - \frac{5 F_{z} \left(4 + 3 \sqrt{2}\right)}{16 \pi \left(2 \sqrt{2} + 3\right)}\\- \frac{5 F_{z} \left(2 \sqrt{2} + 3\right)}{24 \pi \left(7 + 5 \sqrt{2}\right)} & - \frac{F_{z} \left(11 \sqrt{2} + 16\right)}{16 \pi \left(7 + 5 \sqrt{2}\right)} & 0\\- \frac{5 F_{z} \left(4 + 3 \sqrt{2}\right)}{16 \pi \left(2 \sqrt{2} + 3\right)} & 0 & - \frac{F_{z} \left(103 \sqrt{2} + 148\right)}{48 \pi \left(7 + 5 \sqrt{2}\right)}\end{matrix}\right]\end{split}\]

Visualization of the fields

Since it is difficult to handle these lengthy expressions we can visualize them. For that, we define a grid where to evaluate the expressions,

\[(x, z) \in [-2, 2]\times[0, 5]\, ,\]

in this case.

x_vec, z_vec = np.mgrid[-2:2:100j, 0:5:100j]

We can use lambdify() to turn the SymPy expressions to evaluatable functions.

def field_plot(expr, x_vec, y_vec, z_vec, E_val, nu_val, Fx_val, Fz_val, title=''):
    """Plot the field"""

    # Lambdify the function
    expr_fun = lambdify((x, y, z, E, nu, Fx, Fz), expr, "numpy")
    expr_vec = expr_fun(x_vec, y_vec, z_vec, E_val, nu_val, Fx_val, Fz_val)

    # Determine extrema
    vmin = np.min(expr_vec)
    vmax = np.max(expr_vec)
    print("Minimum value in the domain: {:g}".format(vmin))
    print("Maximum value in the domain: {:g}".format(vmax))
    vmax = max(np.abs(vmax), np.abs(vmin))

    # Plotting
    fig = plt.gcf()
    levels = np.logspace(-1, np.log10(vmax), 10)
    levels = np.hstack((-levels[-1::-1], [0], levels))
    cbar_ticks = ["{:.2g}".format(level) for level in levels]
    cont = plt.contourf(x_vec, z_vec, expr_vec, levels=levels,
                        cmap="RdYlBu_r", norm=colors.SymLogNorm(0.1))
    cbar = fig.colorbar(cont, ticks=levels[::2])
    cbar.ax.set_yticklabels(cbar_ticks[::2])
    plt.axis("image")
    plt.gca().invert_yaxis()
    plt.xlabel(r"$x$")
    plt.ylabel(r"$z$")
    plt.title(title)
    return cont

Displacements

plt.figure()
field_plot(u.norm(), x_vec, 0, z_vec, 1.0, 0.3, 0.0, 1.0)
plt.show()
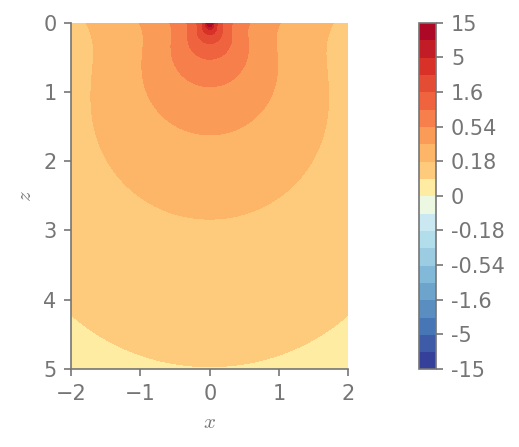
../_images/point_source_umag.png 
Minimum value in the domain: 0.0881197
Maximum value in the domain: 15.4645

plt.figure()
field_plot(u[0], x_vec, 0, z_vec, 1.0, 0.3, 0.0, 1.0)
plt.show()
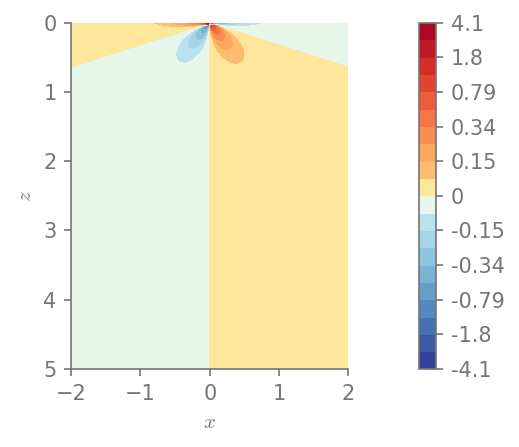
../_images/point_source_ux.png 
Minimum value in the domain: -4.09665
Maximum value in the domain: 4.09665

plt.figure()
field_plot(u[2], x_vec, 0, z_vec, 1.0, 0.3, 0.0, 1.0)
plt.show()
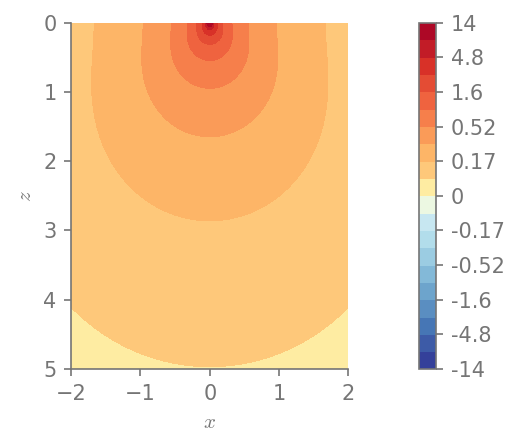
../_images/point_source_uz.png 
Minimum value in the domain: 0.0869101
Maximum value in the domain: 14.3383

Stresses

We can plot the components of stress

for row in range(0, 3):
    for col in range(row, 3):
        plt.figure()
        field_plot(stress[row,col], x_vec, 0, z_vec, 1.0, 0.3, 0.0, 1.0,
                   title=r"$\sigma_{%i%i}$"%(row+1, col+1))

plt.show()
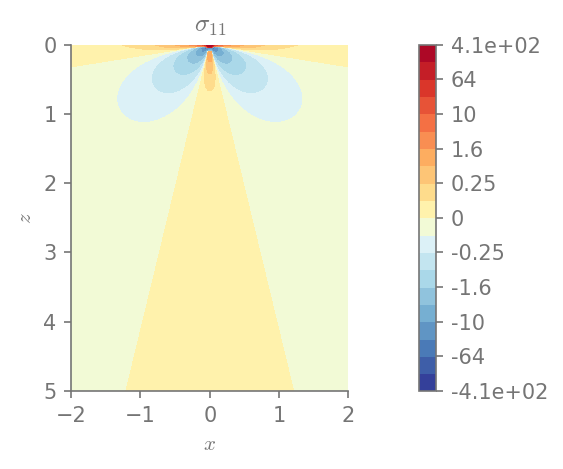
../_images/point_source_σ11.png 
Minimum value in the domain: -41.4274
Maximum value in the domain: 406.682
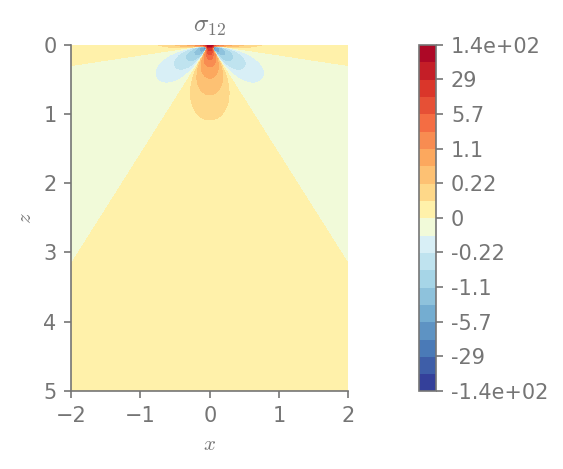
../_images/point_source_σ12.png 
Minimum value in the domain: -12.0021
Maximum value in the domain: 144.846
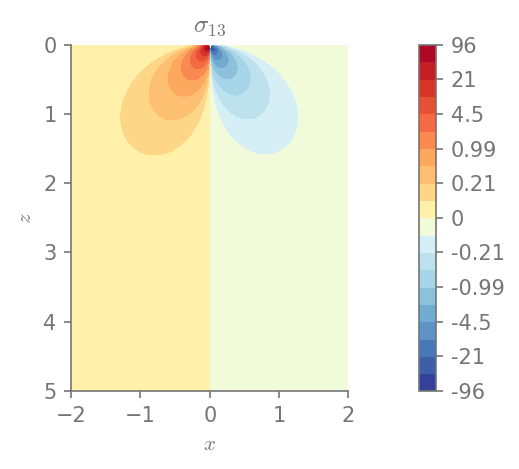
../_images/point_source_σ13.png 
Minimum value in the domain: -95.9472
Maximum value in the domain: 95.9472
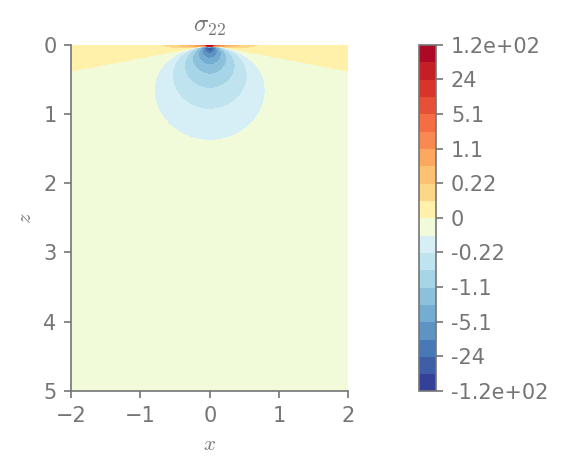
../_images/point_source_σ22.png 
Minimum value in the domain: -59.0538
Maximum value in the domain: 116.991
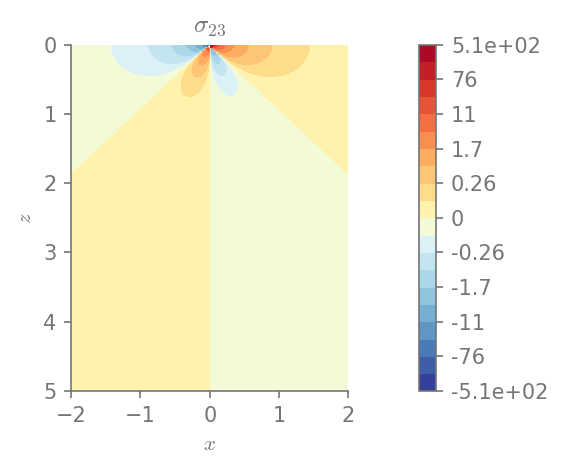
../_images/point_source_σ23.png 
Minimum value in the domain: -506.96
Maximum value in the domain: 506.96
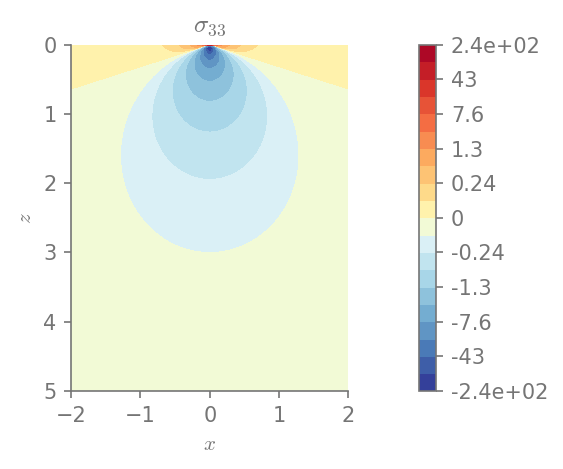
../_images/point_source_σ33.png 
Minimum value in the domain: -243.272
Maximum value in the domain: 116.991

Stress invariants

We can also plot the invariants of the stress tensor

I1 = S(1)/3 * stress.trace()
I2 = S(1)/2 * (stress.trace()**2 + (stress**2).trace())
I3 = stress.det()
Mises = sqrt(((stress[0,0] - stress[1,1])**2 + (stress[1,1] - stress[2,2])**2 +
             (stress[2,2] - stress[0,0])**2 +
             6*(stress[0,1]**2 + stress[1,2]**2 + stress[0,2]**2))/2)

plt.figure()
field_plot(I1, x_vec, 0, z_vec, 1.0, 0.3, 0.0, 1.0)
plt.show()
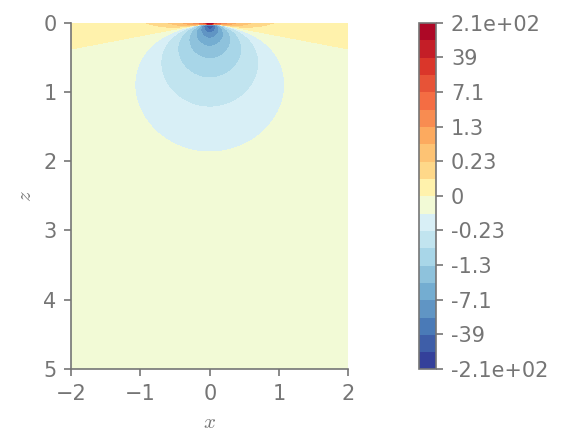
../_images/point_source_I1.png 
Minimum value in the domain: -107.797
Maximum value in the domain: 213.555

plt.figure()
field_plot(I2, x_vec, 0, z_vec, 1.0, 0.3, 0.0, 1.0)
plt.show()
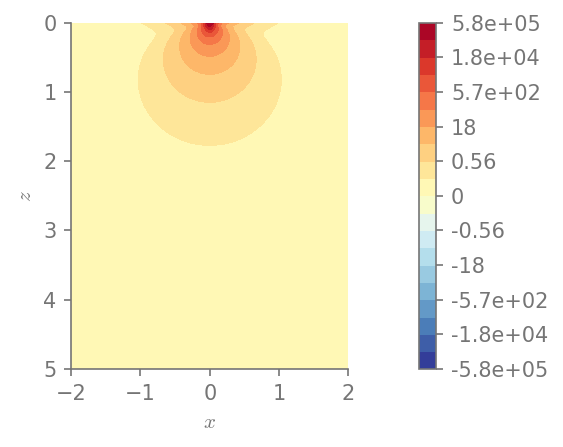
../_images/point_source_I2.png 
Minimum value in the domain: 0.000977492
Maximum value in the domain: 579596

plt.figure()
field_plot(I3, x_vec, 0, z_vec, 1.0, 0.3, 0.0, 1.0)
plt.show()
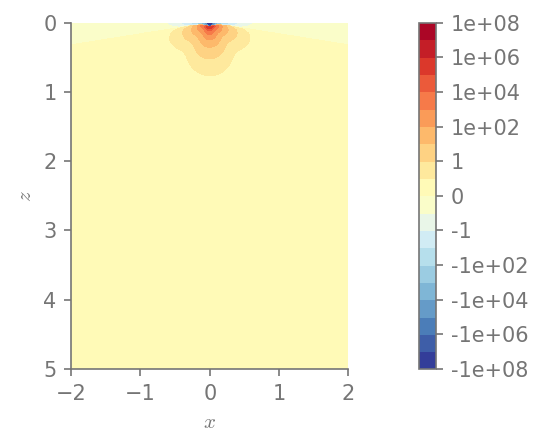
../_images/point_source_I3.png 
Minimum value in the domain: -1.01409e+08
Maximum value in the domain: 419218

plt.figure()
field_plot(Mises, x_vec, 0, z_vec, 1.0, 0.3, 0.0, 1.0)
plt.show()
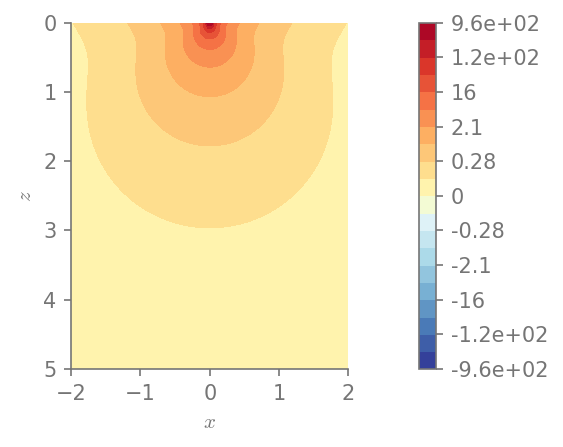
../_images/point_source_mises.png 
Minimum value in the domain: 0.0274784
Maximum value in the domain: 958.065

References

[LANDAU]
Landau, L. D., Kosevich, A. M., Pitaevskii, L. P., & Lifshitz, E. M.
(1986). Theory of elasticity.